El aleteo de una mariposa

Algunos avances importantes en las matemáticas recientemente publicados permiten abordar la mejora de procesos cotidianos

Recientemente se ha publicado el libro ‘Sobre la topología y la estabilidad futura del Universo’, del matemático sueco Hans Ringström, en el que se presentan unos resultados extraordinarios. Aunque los detalles están solo al alcance de los especialistas, sin embargo, hay tres aspectos cuya comprensión están al alcance de cualquiera.

En primer lugar, el concepto de estabilidad y por qué es importante. En segundo lugar, qué tiene que esto que ver con la teoría del caos. Y finalmente, cómo estas herramientas desarrolladas pueden servir para mejorar, por ejemplo, la tecnología.

¿Qué es eso de la estabilidad?

Pongamos por ejemplo un medicamento. Un paciente tiene que tomar cierta dosis de ese medicamento. ¿Qué ocurre si toma un poco más o un poco menos? Para que un medicamento sea seguro debería de ocurrir más o menos lo mismo que si se toma la dosis exacta. Sería un desastre si por un descuido tomase un poco más y eso ya significase una sobredosis. Esto en lenguaje matemático se describiría como que la solución es estable ante pequeñas perturbaciones.

En economía, consideraciones de este tipo son fundamentales también. Si uno tiene una hipoteca asociada al valor del euro, no sería bueno si una pequeña variación del valor del euro hiciese que de pronto uno fuese incapaz de pagar la mensualidad. En este caso lo que se quiere es que el pago de la mensualidad sea estable ante variaciones pequeñas del valor del euro.

Sin embargo cuando se desarrolló la teoría del caos, los matemáticos se dieron cuenta estudiando muchos sistemas que la norma es la inestabilidad y no la estabilidad de soluciones. Esa inestabilidad es una de las propiedades más importantes que caracterizan las soluciones caóticas.

Teoría del caos

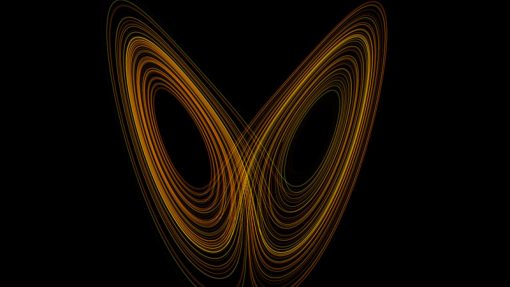
Desde sus inicios, la teoría del caos ha estado asociada a la imagen del efecto de un aleteo de una mariposa en la previsión del tiempo. El meteórologo y matemático estadounidense Edward Lorenz al estudiar las ecuaciones que rigen ciertos procesos del clima, se dió cuenta que en determinadas situaciones un pequeño cambio en las condiciones iniciales podía tener un efecto dramático en cómo se comportaba el clima.

Desde que se dió este descubrimiento se han desarrollado muchas herramientas matemáticas para explorar este efecto en todo tipo de fenómenos físicos complejos y poder llegar a conclusiones, incluso cuando el proceso es altamente inestable.

Hoy en día a la teoría del caos se le llama más bien teoría de los sistemas dinámicos, porque ahí donde hay algo dinámico, es decir donde hay movimiento, ocurren ‘fenómenos dramáticos’. Son la regla y no la excepción. De fondo lo que hay es el estudio de pequeños cambios en la cantidad, que conllevan o no a un cambio en la calidad.

¿Principio cosmológico o resultado dinámico?

Una situación compleja es el análisis de la dinámica del Universo en su conjunto. Ese campo se llama cosmología y nació gracias a la teoría de la relatividad general de Einstein. Para modelar el cosmos generalmente se parte de una hipótesis muy fuerte y es que el Universo es ‘homogéneo e isótropo’, es decir, se asume la idea de que cualquier punto y cualquier dirección del Universo son equivalentes. Estemos en una galaxia muy lejana o en la nuestra, las propiedades deben ser la mismas: la misma densidad de masa, la misma presión… A esto se le da el nombre de principio cosmológico.

Sin embargo se sabe que el Universo en realidad no es completamente homogéneo, como muestra la imagen de la radiación de fondo de microondas. Esta imagen es un foto térmica de la radiación que nos llega desde todas partes. La diferencia de temperatura de la radiación de fondo que se recibe de diferentes direcciones en la Tierra es de 0.00001 grados Celsius. Esto es una buena indicación de que el Universo aunque no sea homogéneo, lo es de forma aproximada, porque apenas hay variación en la temperatura de la radiación. Así, asumiendo la homogeneidad, los físicos han podido empezar a hacer cálculos y obtener unas primeras conclusiones.

Ahora bien, todas las conclusiones importantes del modelo estándar de cosmología se basan en que el principio cosmológico se cumple de forma exacta, es decir, que se asume que el Universo es exactamente homogéneo. ¿Las conclusiones importantes siguen siendo válidas si esto no fuera exactamente así?

Aplicando la teoría del caos al cosmos

Lo que ha hecho Hans Ringström en su libro, es coger la solución que corresponde a un Universo homogéneo y considerar ligeras perturbaciones, es decir ‘aleteos de mariposa’, y ver si se obtienen los mismos resultados cualitativos que asumiendo un cosmos completamente homogéneo. Es decir, volviendo al simil del medicamento, ver si un ligero aumento en la dosis lleva a un cambio importante en la reacción del paciente o no. Ver si unas posibles inhomogeneidades en el cosmos cambian las conclusiones a las hasta que ahora llegaban los físicos, o si el modelo es estable.

En toda su generalidad no ha sido posible demostrarla, pero en este libro científico, de más de 700 páginas llenas de cálculos y teoremas, de Hans Ringström, se ha obtenido un resultado bastante general demostrando que perturbaciones del modelo no cambian las conclusiones cualitativas. Esto es un gran respaldo a la teoría hasta ahora aceptada.

Resumiendo, conforme a estos últimos resultados matemáticos, la respuesta a si un aleteo de una mariposa puede cambiar el destino del Universo es no. Sin embargo, hasta que no se haya demostrado en todo su generalidad la mariposa puede tener más poder de lo esperado y el cosmos puede ser un sistema mucho más inestable de lo que se cree actualmente.

Aunque aquí hayamos hablado de un resultado matemático muy especializado, las herramientas matemáticas que se van desarrollando se pueden aplicar a todo tipo de procesos donde nos preguntemos sobre la estabilidad de cierta solución. ¿Cuánto combustible tiene que tener un avión para que el vuelo sea seguro pase lo que pase? ¿Cuánto margen de error tengo antes de que ocurra algo indeseado?

No hay que olvidar que una de las conclusiones fuertes de los matemáticos y la teoría del caos es que la inestabilidad es mucho más mayoritaria de lo que parece. Algunos lo pueden llamar caos, pero hay otra visión que entiende que detrás de la aparente calma, estabilidad o equilibrio, de muchos procesos o situaciones hay muchas más posibilidades de lo que parece. A veces un aleteo de mariposa puede crear un huracán, o como dice la sabiduría popular, la gota colma el vaso o la chispa incendia la pradera.